Magazine: Hello world
Hands-on introduction to genetic programming
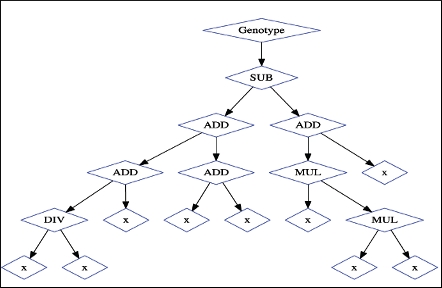
Hands-on introduction to genetic programming
Full text also available in the ACM Digital Library as PDF | HTML | Digital Edition
Thank you for your interest in this article. This content is protected. You may log in with your ACM account or subscribe to access the full text.
Pointers
Code for Hands-On Introduction to Genetic Programming
Pick up the code for this article here:
http://xrds.acm.org/helloworld/2010/08/genetic-programming.cfm